1. cos x = a
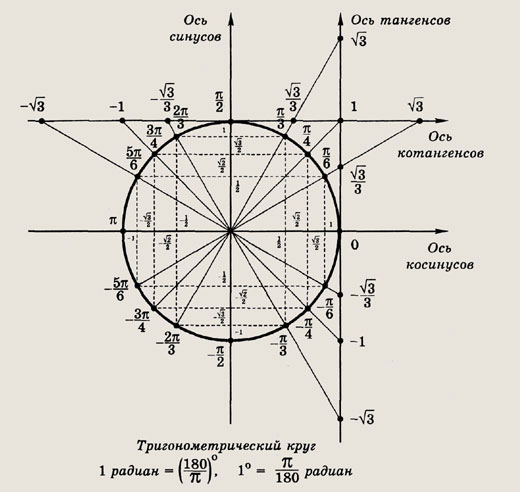
Розв’язки рівняння шукатимемо, спираючись на рисунок 1 або на рисунок 2.
шукатимемо, спираючись на рисунок 1 або на рисунок 2.
Якщо , розв’язків немає.
, розв’язків немає.
 ,
,  ,
,  .
.
 ,
,  ,
,  .
.
 ,
,  ,
,  .
.



Рис. 2
Загальний випадок :
:  , x = ±arccosa + 2πn,
, x = ±arccosa + 2πn, .У випадках, коли
.У випадках, коли  ,
,  , теж можна користуватися загальною формулою, але це не так раціонально.
, теж можна користуватися загальною формулою, але це не так раціонально.
Розв’язки, які описуються загальною формулою, можна поділити на дві серії:
x1 = arccosa + 2πn, n Є Z;
x2 = -arccosa + 2πn, n Є Z.
2. sin x = a
Розв’язки шукатимемо, спираючись на рисунок 1 або на рисунок 2.
Якщо , розв’язків немає.
, розв’язків немає.
 ,
,  , n Є Z.
, n Є Z.
 ,
,  , n Є Z.
, n Є Z.
 ,
,  , n Є Z.
, n Є Z.
Загальний випадок :
:

 , k Є Z.
, k Є Z.

Рис. 1

Рис. 2
Множина розв’язків розбивається на дві серії:
k = 2n, x1 = arcsina + 2πn, n Є Z;
k = 2n + 1, x2 = π – arcsina + 2πn, n Є Z.
3. tg x = a
Розв’язки запишемо, спираючись на рисунок зліва або на рисунок справа нижче.
 , n Є Z.
, n Є Z.

4. ctg x = a
 , n Є Z.
, n Є Z.
Якщо a = 0, , n Є Z.
, n Є Z.
Якщо , можна звести дане рівняння до рівняння
, можна звести дане рівняння до рівняння  .
.
Приклади1) ;
;
 ;
;
 , k Є Z;
, k Є Z;
 , k Є Z;
, k Є Z;
 , k Є Z;
, k Є Z;
 , k Є Z.
, k Є Z.
Множину розв’язків можна розбити на дві серії:
 , n Є Z;
, n Є Z;
 , n Є Z;
, n Є Z;
 , n Є Z;
, n Є Z;
 , n Є Z.
, n Є Z.
2) ;
;
 ;
;
 , n Є Z;
, n Є Z;
 , n Є Z;
, n Є Z;
 , n Є Z;
, n Є Z;
 , n Є Z.
, n Є Z.
Розв’язки рівняння
 шукатимемо, спираючись на рисунок 1 або на рисунок 2.
шукатимемо, спираючись на рисунок 1 або на рисунок 2.Якщо
 , розв’язків немає.
, розв’язків немає. ,
,  ,
,  .
. ,
,  ,
,  .
. ,
,  ,
,  .
.


Рис. 2
Загальний випадок
 :
:  , x = ±arccosa + 2πn,
, x = ±arccosa + 2πn, .У випадках, коли
.У випадках, коли  ,
,  , теж можна користуватися загальною формулою, але це не так раціонально.
, теж можна користуватися загальною формулою, але це не так раціонально.Розв’язки, які описуються загальною формулою, можна поділити на дві серії:
x1 = arccosa + 2πn, n Є Z;
x2 = -arccosa + 2πn, n Є Z.
2. sin x = a
Розв’язки шукатимемо, спираючись на рисунок 1 або на рисунок 2.
Якщо
 , розв’язків немає.
, розв’язків немає. ,
,  , n Є Z.
, n Є Z. ,
,  , n Є Z.
, n Є Z.
 ,
,  , n Є Z.
, n Є Z.Загальний випадок
 :
:
 , k Є Z.
, k Є Z.
Рис. 1

Рис. 2
Множина розв’язків розбивається на дві серії:
k = 2n, x1 = arcsina + 2πn, n Є Z;
k = 2n + 1, x2 = π – arcsina + 2πn, n Є Z.
3. tg x = a
Розв’язки запишемо, спираючись на рисунок зліва або на рисунок справа нижче.
 , n Є Z.
, n Є Z.
4. ctg x = a
 , n Є Z.
, n Є Z.Якщо a = 0,
 , n Є Z.
, n Є Z.Якщо
 , можна звести дане рівняння до рівняння
, можна звести дане рівняння до рівняння  .
.Приклади1)
 ;
; ;
; , k Є Z;
, k Є Z; , k Є Z;
, k Є Z; , k Є Z;
, k Є Z; , k Є Z.
, k Є Z.Множину розв’язків можна розбити на дві серії:
 , n Є Z;
, n Є Z; , n Є Z;
, n Є Z; , n Є Z;
, n Є Z; , n Є Z.
, n Є Z.2)
 ;
; ;
; , n Є Z;
, n Є Z; , n Є Z;
, n Є Z; , n Є Z;
, n Є Z; , n Є Z.
, n Є Z.
Комментариев нет:
Отправить комментарий